Premiere performance by Jenifer Knippel, purple alto saxophone (aka viv) Ashland, OR Nov. 23, 2013

On July 9, 2013 the neurologist Oliver Sacks turned 80. He and his friends made their celebration around the element with the atomic number 80, Mercury. I’m sure that the party was not a let down from last year, although the atomic number of gold is 79.

When I was getting ready to turn 53 later in July 2013, I noted that my upcoming atomic birthday element was to be iodine. I was also thinking about a piece that my friend the saxophonist Jenifer Knippel asked me to write. It was to be for solo saxophone, a purple alto saxophone named Viv, in fact.

I discovered that the word Iodine was derived from the Greek for “violet-colored,” for the color of the element’s vapor. Aha…
The atomic number of an element is the number of electrons that make up the atom of the element. Iodine therefore has 53 electrons. So far so good.
I looked up the number 53 in my handy Penguin Dictionary of Curious and Interesting Numbers (revised) by David Wells (1997). There was the entry, between 52 and 55. I fear that next year, 54 may not be so interesting, at least according to David Wells!

53. The smallest prime number such that the period of its reciprocal is ¼ of the maximum length possible, in this case, ¼ of 53 – 1, or 13. All fractions k/53, where k is a number between 1 and 52, fall into 4 classes, the decimal period of every fraction in the same class being a cyclic permutation of the others in its class.

First, I calculated the 52 occurrences of the fractions k/53, and they do indeed fall into 4 classes, each with its distinctive cyclic permutation of one of four decimal fractions.

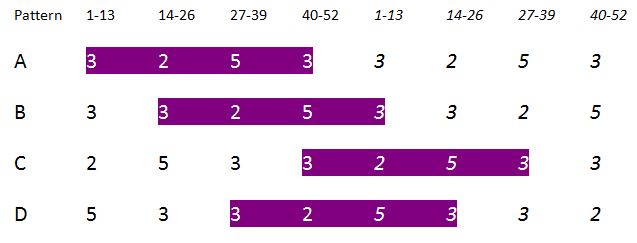
Next I considered them in four sets of 13 fractions each, 1/53 – 13/53, 14/53 – 26/53, 27/53 – 39/53, and 40/53 – 52/53. Each set of 13 fractions showed invariance in that in each there were 2 each of one of the repeating cyclic permutations of decimal fractions, 3 of a second, 3 of a third, and 5 of a fourth.

The pattern of the placement of the 4 classes was also invariant, but “shifted” from one to the next. The following chart shows the patterns twice to depict the “wrap-around” of the basic order. Note the trippy “knight’s move” shift across the four patterns A – D.

This startled me when I discovered it; I was heard to yell “Aha!” in a popular local coffee shop. I shortly realized that all the numbers involved in the counts: 2, 3, 5, 8, and 13 are all consecutive numbers in the Fibonacci series. The barista was very considerate and allowed me to stay as long as I promised to behave.

I now designed a schema with ratio-controlled durations of sections using the above sequences.

(A)3253 (B)3325 (C)2533 (D)5332

 I associated a different musical idea with each of the four patterns except for the “2” sections which received a truncated and invariant version of the “3” sections. The piece was “sequenced” from these four basic ideas in continuous variation. Since the “3” sections usually occur consecutively (once only at the beginning, 3 times in a row from the 4th to the 6th section, and twice elsewhere), they contain the most complex continuously changing music: correlating to the “development” section of a classical sonata. The second half uses the material of the first half mostly in inversion. Taken in pairs, the patterns form a palindrome from beginning to end (I just noticed this today). The different patterns are represented in the piece with a whole-tone melody, a jazzy ballad melody based on the Locrian mode (white keys of the piano from B to B), and a fast and highly chromatic virtuosic tune. You might hear a little bit of “Harlem Nocturne” if you listen a little bit sideways.

Jenifer and viv performed the premiere “in the round,” starting facing away from the audience and slowly turning in place until they were face to face with the audience for the climax of the work. One can image the 53 electrons of the iodine atom orbiting their nucleus as the notes of the piece orbit the performer.

Mark Eliot Jacobs

November 23, 2013